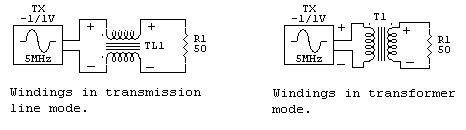
4:1 balun design and operation
|
|
Balun Test Sleeve baluns
|
| EZNEC+ ver. 5.0 ladder line dipole 6/6/2010 7:17:54 PM ————— Source 1 Voltage |
We have 1942 V
RMS differential
mode voltage. This
is what excites the
transmission line in
a 1:1 balun, and
what appears from
terminal to
terminal.
In common mode
from the left
terminal with a
5000 j0 common mode
impedance balun we
have:
| EZNEC+ ver. 5.0 ladder line dipole 6/6/2010 7:05:40 PM ———- LOAD DATA ——– Frequency = 3.6 Load 1 Voltage = Total applied |
With a difficult-to-obtain 5,000 ohm
j0 common mode balun
impedance, the cores
would dissipate 122
watts or 12.2% of
applied power.
There are two
ways to fix this,
make the balun
primarily reactive
or alter the
feed line length.
Looking at a
slightly reactive
balun common mode
from using a higher
Q core:
| EZNEC+ ver. 5.0 ladder line dipole 6/6/2010 7:37:01 PM ————— LOAD DATA ————— Frequency = 3.6 Load 1 Voltage = Total applied |
We can see that
balun core
dissipation would
now increase to 15%
of applied power.
Current unbalance
would also increase
considerably from
.156 amperes to
.1939 amperes.
| EZNEC+ ver. 5.0 ladder line ————— Frequency = 3.6 Load 1 Voltage = Total applied |
Balun common mode
current is up to .25
amperes, the highest
value yet. Balun
heat would be down
to a cool 6 watts.
This balun core
would barely get
warm.
The above is
NOT WORSE
CASE,
just a random case I
picked from typical
feed line lengths. It
is possible for all
of these numbers to
get worse, and for
the addition of a
high-Q balun that is
primarily all
reactance to seriously
unbalance the
antenna system. This is
true even with a
very high reactance!
Many times a cool-running balun is a
sign of a balun not
doing its job.
Typical 80 meter
Doublet on 40 Meters
The typical
80-meter dipole or
doublet on 40 meters
with a 65 foot long
feed line is an
example of another
stressful load for a
balun.
|
ladder line dipole 6/8/2010 11:10:04 AM ————— SOURCE DATA ————— Frequency = 7.2 MHz Source 1 Voltage |
ladder line dipole 6/8/2010 11:10:04 AM ————— LOAD DATA ————— Frequency = 7.2 MHz Load 1 Voltage = Total applied |
By not changing
height of the
antenna, and only
changing feed line
length to 99 feet
(from 1/2 wave above
to approximately 3/4
wavelength), we have
the following:
|
ladder line dipole 6/8/2010 11:30:50 AM ————— SOURCE DATA ————— Frequency = 7.2 MHz Source 1 Voltage |
ladder line dipole 6/8/2010 11:30:46 AM ————— LOAD DATA ————— Frequency = 7.2 MHz Load 1 Voltage = Total applied |
Balun core heat
is reduced from 162
watts or 16% of
transmitter power, to
8 watts or 0.8% of
transmitter power.
feed line length is
critical to optimum
balun performance.
While it isn’t
always the case that
balun heat or core
stress is always low
with a low
terminating
impedance on the
balun, it is
generally true that
balun core stress
always increases
with load impedance
terminating the
balun.
I only use an
air-core choke balun
in very specific
applications where I
know what the effect
will be. When the
system is unknown, I
use a core that
produces a
primarily resistive
common mode
impedance. If the
balun overheats, I
alter feed line
length. This will
often correct the
problem without
changing the balun’s
design.
Some entire balun
handbooks and many
articles have been
written without an
understanding of how
the balun actually
interacts with the
antenna system. The
truth is… if a
balun never
overheats at high
power in any
application, it may
not be acting like a
balun at all with real loads. Some baluns appear perfect on the test bench while
failing to balance many real-world systems.
Range of Common Mode Impedances
One way to measure common mode impedance is to short the feed line terminals
and feed the system as a single wire antenna. Here is the common mode impedance
of another 80-meter doublet or dipole fed with 99 feet of open wire line on 40
meters.
| — common mode source impedance– Frequency = 7.2 MHz Impedance = 98.86 – J 272.3 ohms |
5000 j0 CM balun losses
Load 1 Voltage = 216.4 V at -123.54 deg. Total applied power = 1000 watts Total load power = 9.363 watts |
–differential mode SOURCE DATA — Frequency = 7.2 MHz (400 ohm system) = 5.359
|
We see that when common mode and differential source impedances are
low, a balun can do a very effective job. feed line common mode impedance can
range from a few ohms to several thousand ohms, and this impedance critically
affects balun and system performance. If we insert a balun at a point driven
with very high voltages balun heating can be catastrophic. If the balun doesn’t
heat, from inadequate common mode impedance or being largely reactive, the system will
often just go out of
balance.
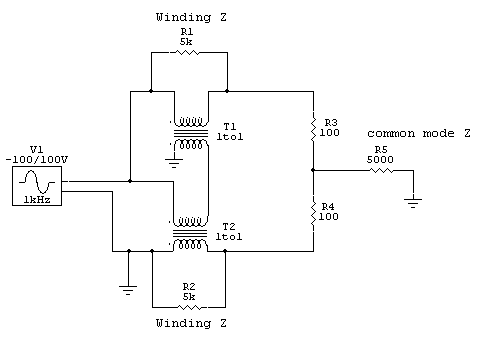
4:1 Transmission Line Balun with Balanced Load
The circuit below shows a 4:1 transmission line current balun in operation feeding a balanced
load. This
balun is a 4:1 ratio
and feeds a balanced
200-ohm load. This
load would be very
similar to the
terminal impedances
of a full-size
perfectly
symmetrical antenna,
like a folded dipole, a large and
perfectly
symmetrical loop, or
a symmetrical “T”
matched antenna with
a feed line length
that is neither
worse case nor
optimum feed line
length.
The load resistors
have to be grounded
in the center for
one simple reason.
For any system to be
perfectly balanced,
or for a balanced
transmission line to
not radiate, line
currents have to be
exactly equal and
opposite and voltage
with respect to the
outside world has to
be exactly equal and
opposite at any and
all points along the
system. Many people
miss this, and think
the only requirement
is having equal and
opposite currents at
one point in the
system is enough to
ensure full system
balance.
Another serious flaw is testing a balun or analyzing a balun using a floating
load, like a physically small resistor placed across balun output terminals. One
popular UnUn and Balun handbook shows a lack of understanding of how to analyze,
measure, and test baluns! It actually suggests power is evenly divided between
the two choke baluns making up a 4:1 current balun. Nothing is further from the
truth! Most likely the misconception that the transformers share equal
dissipation comes from a lack of understanding of field theory and antenna
systems, especially common mode impedances.
Let’s look at power dissipation using a SPICE model. Logic tells us with an
infinite common mode load impedance (R5), like a physically small resistor,
balun voltage and heating will be equal in each winding:
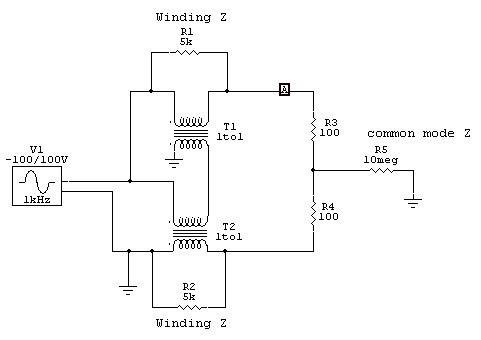
This model uses a 10 million ohm common mode impedance, allowing the magnetizing
impedance in transformers T1 and T2 to determine voltage division. With equal
transformers, voltage will divide evenly. This is the flawed case used by some
balun designers and published in some balun handbooks and white papers.
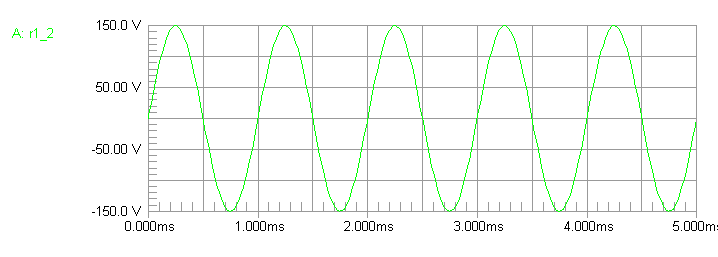
We see the model agrees with theory.
Balun upper and lower terminal voltages are in a 3:1 ratio, and the sum of
voltages equals balun source voltage.
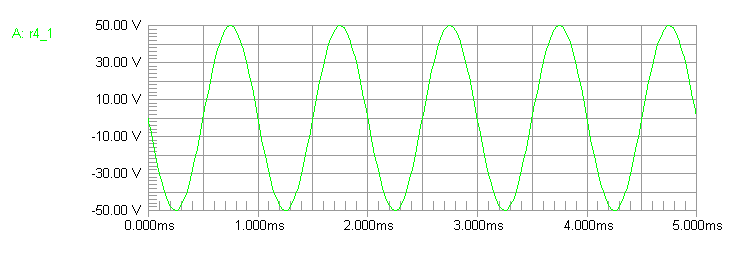
Balun core dissipation would only be 1/2 watt in each core with 200 watts
delivered to the 200-ohm load.
Core heating and dissipation is evenly split.
Now let’s look that the upper extreme common mode impedance likely to occur
in real-world systems:
In this case we set common mode Z at 5000 ohms. This would be similar to a
1/4 wave long open wire line feeding a large matched balanced load, like a
folded dipole antenna.
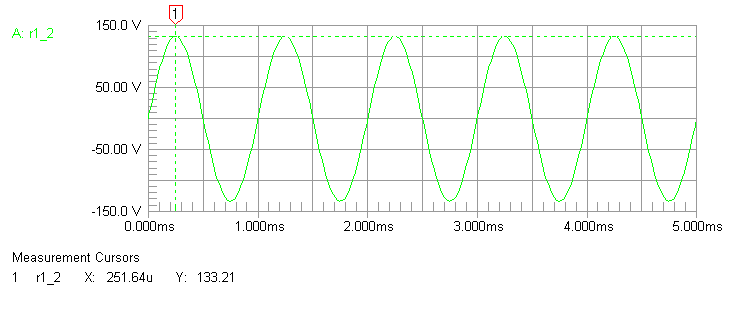
Upper terminal R3 top is 133.2 volts.
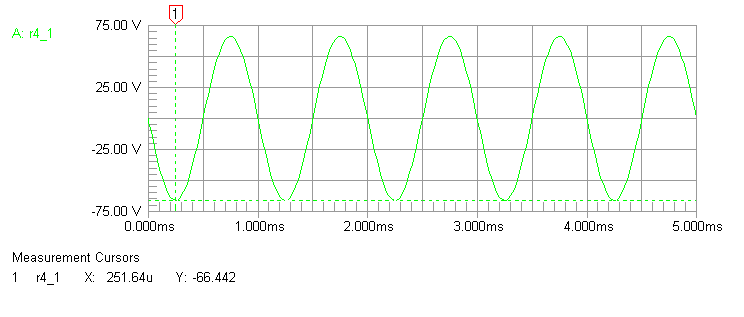
Lower terminal voltage is now 66.44 volts, now a ratio of only 2:1 in
voltages. Balun cores are now unevenly heated, with 223 mW dissipation in the
top core (T1) and 883 mW dissipation in the bottom core (T2).
This is still a successful balun because the applied voltage is so low, but
it demonstrates how uneven core heating increases rapidly with very slight
amounts of common mode current. T2 heats four times more than the other core,
T1!
Running through the model again but with a 650-ohm common mode impedance, a
very typical middle for common mode impedance, we again find uneven core heating
becomes a problem. The system has only 21 milliwatts
in T1, and 1.61 watts in T2. This is a core heating ratio
of 77:1 between the two core!!! The upper core barely does anything.
A second factor in heating is the voltage across the load resistance, R3 and
R4. In this case we only have 200 volts across the resistors because we have a
1:1 load SWR (200 ohm load across an assumed 200 ohm balun output) at 200 watts.
If the feeder has a high SWR, like a 450-ohm line feeding a dipole or doublet
antenna, and if we pick a combination of antenna and feed line length that
present a high load impedance to the balun, we can have severe balun heating
problems even with modest power. This is because balun core losses are so high.
This tells us there are two general rules for minimizing balun heating:
- Common mode impedance should be as high as possible on the balun output.
- Differential mode impedance should be as low as possible across the
balun output.
We can also conclude any balun test that assumes equal distribution of losses
between cores is an impossible real-world situation. There isn’t an antenna system
anywhere that has an infinite common mode impedance, and virtually every system
is under 5000 ohms common mode impedance. Most antenna systems are probably 1000
ohms or less common mode impedance, so we can just ignore any contribution of
the upper transformer to power handling.
article is soon to follow showing measured data. 7/23/2010
This also excludes the idea that a dual transmission line balun like a 4:1
can use a single core, an idea that was promoted in a popular Balun and UnUn
handbook. The flawed idea the load looks like a floating resistor results in all
sorts of misunderstandings about balun behavior.
My Earlier Simple Models and Analysis
This is an earlier model I used, and the method I use on the
test bench here. It is easy to see it is much closer to the real world than the
floating resistor (infinite common mode impedance) model. As a matter of fact if
every system presented infinite common mode impedance to the balun, there would
be no need for baluns in any system!
In this balun,
the transmission
line transformers
clearly behave in
two very distinct
modes. They act as
1:1 transformers,
and they also act as
transmission lines.
In the first
example, one of
perfect balance, the
transmission line
transformers operate
primarily as
transformers. T2 is
excited across
e-f by 10
volts with g-h
being the secondary,
while T1 is excited
by theoretically
exactly equal and
opposite currents in
the windings and
thus has zero core
flux density.
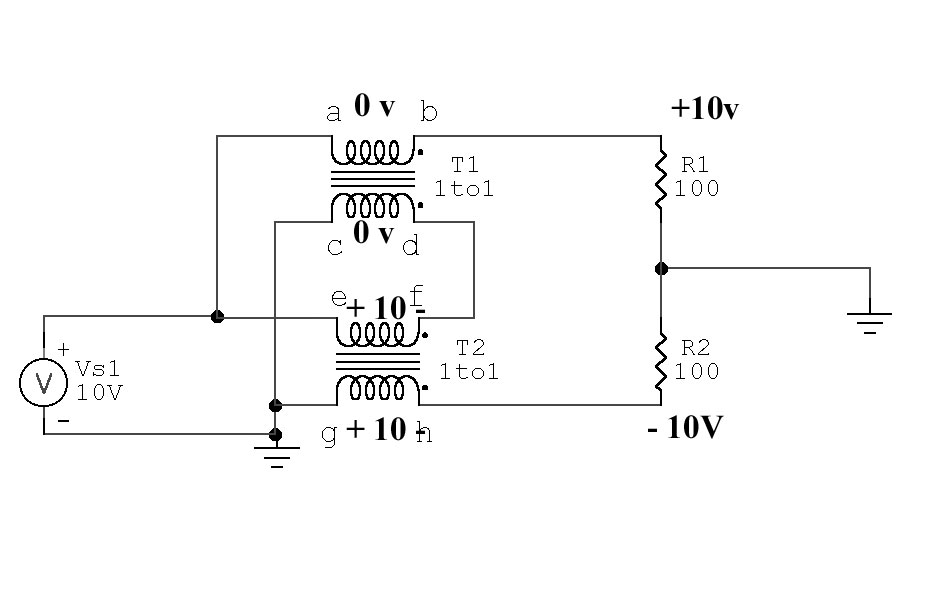
T1 voltages and currents:
Current flowing through
a-b is 0.1 ampereCurrent flowing through
c-d
is 0.1ampere in
the opposite
direction
This results in zero voltage across
a-b and
c-d
Volt-turns in T1 is zero under
a perfectly balanced condition, since current in windings
flows opposite directions. R1 current through
a-b is equaled by T1 from
d-c, so
ampere turns magnetizing
the core oppose each
other. T1 has no flux in core, since volt-turns =
zero. T1 can be shorted from
a-b or from
c-d with no effect.
T2 voltages and currents:
e-f has the same current as flows through
c-d,
c-d has the same as a-b,
0.1 ampereg-h must also have the same current as flowing through
e-fR2 has equal current with R1, 0.1 ampere
this means g-h has 10 volts, phase as shown
Ampere turns (flux density) in T2 is R2 current times turns. T2 core carries
all the flux in a balanced-voltage balanced-current (perfect balance) condition.
Real Transmission Line 4:1 Balun Unbalanced Voltage R1 top =0V
The same balun with perfect unbalance in load, top grounded:
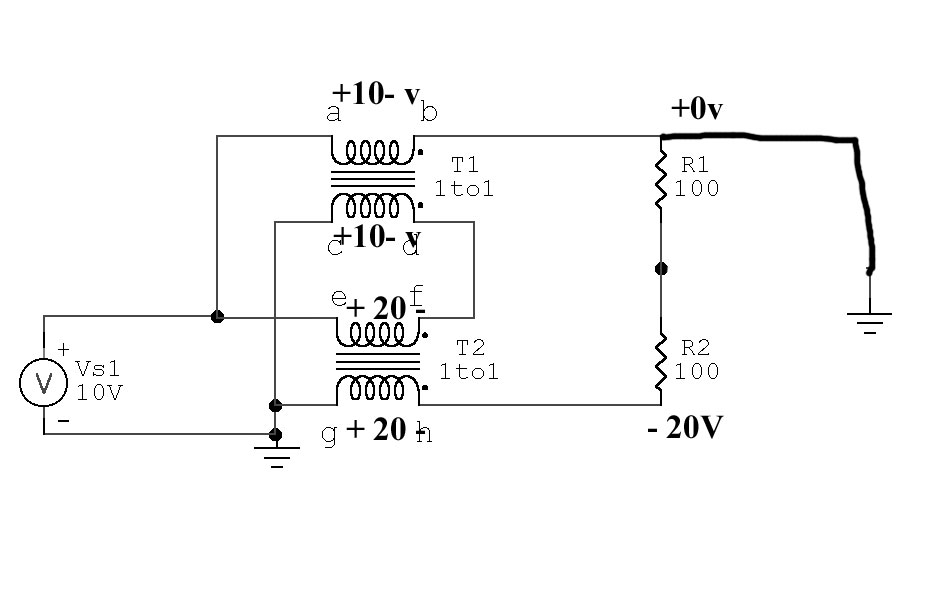
In this case we
new voltages.
T2 now has twice
the volt-turns of
T1, and with equal
windings and cores
this causes flux density in T2
to be twice that of T1.
T1 cannot be
replaced by a short
from a-b
or c-d.
T1 is now required to allow voltage at top of R1 to
deviate from the
original +10 volts,
in this case
reaching 0 volts. .
Shorting a-b or
g-h would
now prevent proper operation.
Real 4:1 Transmission Line 4:1 Balun Bottom Grounded
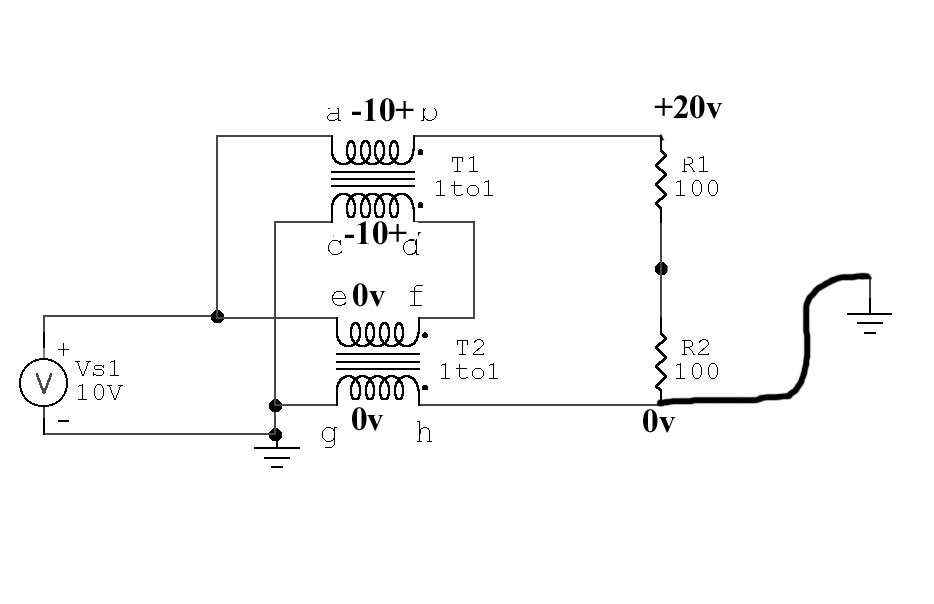
Now we see flux density in T2 is zero.
g-h or
e-f can be shorted
Flux density in T1 is maximum, flux in T2 is zero.
Single-Core Dual Transmission Line Balun
It has been proposed
in a few places that a single core can be used
to create two 1:1 choke baluns in a
transmission line balun, and
this will still
create a good current balun.
We cannot combine
cores
unless each transformer has IDENTICAL flux density
under all conditions
of load balance.
Here’s what happens to our baluns above if we have a
single core that provides a
closed path for all flux
from all windings:
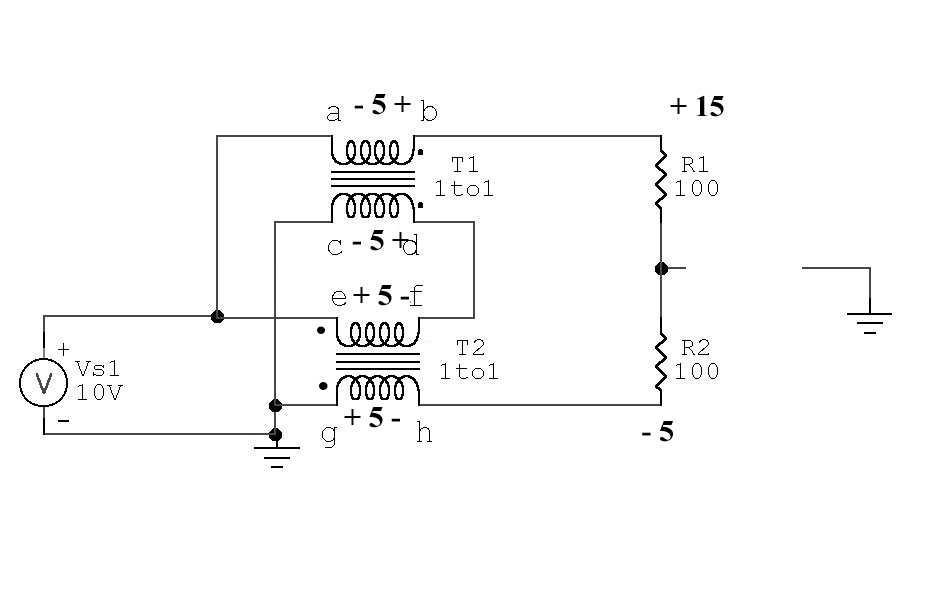
With identical turns on each
winding and a common core
causing equal flux
levels to pass through
every winding,
voltage across each winding
would be held equal. This means any solution
of voltages to the load must provide:
The sum of voltages from
c to e must equal supply voltage
Output voltage across load is now 20v, so we have a correct 4:1 impedance
ratio but:
Load is voltage unbalanced, that means if we ground center tap or either
end of the load we upset voltages and currents in the system. We no longer
have a balun, we have an unbalanced voltage source.
Any tolerance of the three balance conditions a current balun must
maintain would only occur if the core had flux leakage. The worse the core, the
better the balun will behave.
The book
Baluns and UnUn’s proposes a transmission line balun like the balun above could be wound
on a single core. That isn’t true. A balun configured as
shown to the left must be on two
separate cores or it will not remain balanced.
We cannot hold each
core to the same
flux density or the
load will be
seriously
unbalanced.
The source end of the transmission line must always be fed with equal and
opposite currents, and must always have the source applied in differential
across the line at the input (source end) only.
In a transmission line (excited as shown above) energy is conveyed from
end-to-end in a TEM mode. This mode requires, under the conditions of matched
load, voltage between conductors along the line to be in a precise relationship
with current. In the case of a 50 ohm line with 50 watts, current (through
vector) would be 1 ampere while voltage (across vector) would be 50 volts. This
is true anywhere along the line.
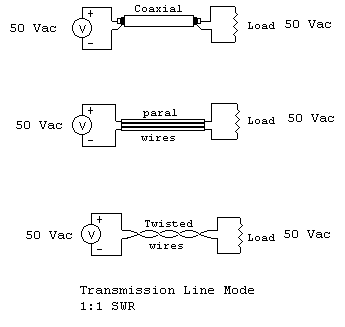
If we mismatch the line, the product of voltage across and current
through the line at any point is still 50, even though the ratio of E to I will
change.
We have two conditions then that apply to any load.
- In a matched condition voltage across and current through at any point are
always in the same ratio, and that ratio equals line impedance and the product
always equals power applied. Transmission currents in the two conductors are
always exactly equal and opposite
at any single
point along the
line. - In a mismatched line the voltage across and current through the line at any
point has a vector product equal to power applied, and the ratio of voltage and
current at any point is equal to the line operating impedance at that point.
Transmission currents are always equal and opposite.
Here is a way
to have equal
currents but not be
in a transmission
line mode:
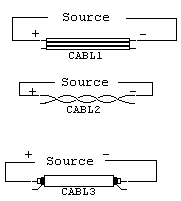
If we take the output from the conductor normally used as the opposing conductor in
a transmission line,
we still have
opposing current
directions. The electrical equivalent of
this “transmission
line” circuit is shown here:
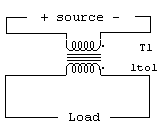
This obviously is not a transmission line
mode, but instead is a simple basic
primary/secondary transformer.
Let’s see if this system follows the same rules as a transmission line in TEM
mode.
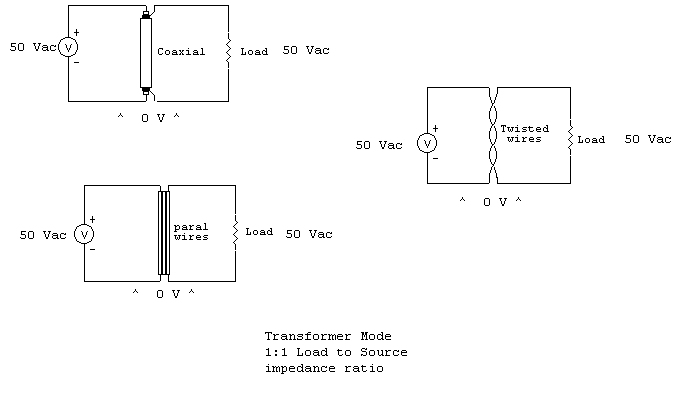
Notice in all cases above voltage across the line at any and all points is
zero. This means no energy is conveyed along the line in TEM (transmission line)
mode, even though currents are exactly equal and opposite. This system does
follow the basic rules of a conventional transformer, in that the secondary
ampere-turn product always equals primary-ampere turn product in order to keep
secondary magnetic flux in equilibrium with primary flux density.
For example, if we have a lossless one turn primary and two turn secondary
transformer with one ampere flowing in the primary, we know we must have 1/2
ampere in the two-turn secondary. This is independent of impedance between
conductors.
In TEM mode, in a matched condition, the across and through vectors (E and I)
at any point multiply to give us power flowing past that point. In
“transformer mode”,
the product is zero
because voltage
between conductors
is at any point is
zero. We can change
even “line
impedance”, and the
change will have
very little effect
on SWR!
In transformer
mode:
- Instead of energy being conveyed to the load by conduction currents
flowing through a direct wired path (as in a transmission line balun),
energy is now transferred through the “balun” via flux coupling
between conductors. This means the balun core is
at least partially involved in all energy
transfer. - The fact the core is directly subjected to magnetizing forces and is
excited directly by source voltage greatly limits power/ mismatch range of
the balun. A normal transmission line balun can tolerate extreme mismatches
if proper materials are used, but the same size and quality materials in a
transformer-style balun handle less power into matched loads, and
significantly less power into highly mismatched
loads. - In a normal transmission line (even one used in a balun) the series
inductance of the conductors is balanced by the shunting capacitance between
the conductors. This means if we terminate the transmission line correctly,
VSWR bandwidth is extremely wide.
since June 12 2005