How the PA Tube
Converts DC anode
voltage to Radio
Frequency
Power

A
typical vacuum tube
radio-frequency
amplifier has a high
voltage power
source. This power
source supplies the
energy for the RF
output power. The
vacuum tube acts
like a non-linear
time-varying resistance
in series with a
diode. The
electrical
equivalent of the
anode and output
system is:

 

  

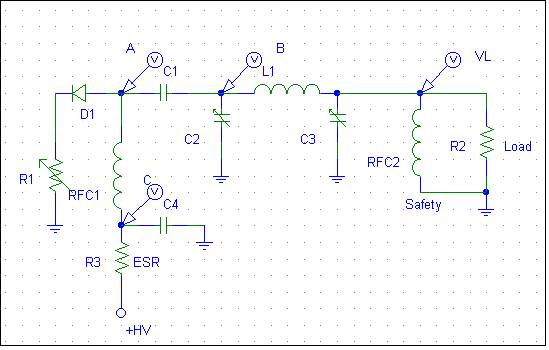
R1
represents the
time-varying anode-to-cathode
resistance of the
output device. As
grid-cathode and
anode-cathode
voltage changes, R1’s
value changes.

D1
represents the
directional
characteristics of
the tube
anode-to-cathode
current path. D1 is always
“on” when the
voltage at point “A”
is more positive
than ground. D1
would also behave as
a current limiter,
the current always
having to be
something less than
the saturated
emission current of
the cathode. The
only exception to
this is if the tube
shorts or arcs
internally.

 

 

 

 

 

 

Let’s
examine how this
circuit converts DC
to RF power. We will
assume +HV is 3000
volts.

 

In
the initial state,
C1 has been charged
through the
following DC path:

 

 

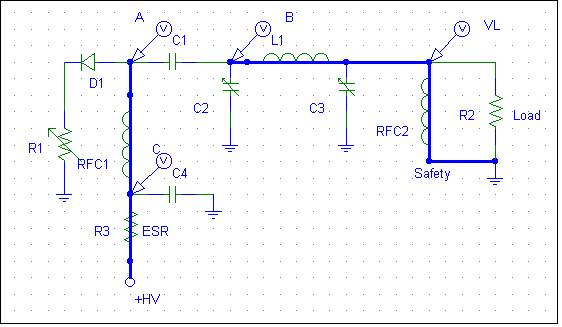
Hopefully
the designer was
smart enough to
include RFC2, to
prevent charging or
discharging C1 into
the load, which
might be a sensitive
piece of gear (or the
operator)!

The
voltage across C1 is
the anode-to-ground
voltage at A, in this case 3000 volts while resting without RF drive power. 
Everything
past A, at B and VL,
is zero volts in the
resting state. This
is
because of the
low-dc resistance of
RFC2 and the nearly
infinite resistance
(and dc impedance) of
capacitor C1. RFC1,
the plate choke,
establishes a fixed
or static magnetic field,
the intensity of
which
is set by the
quiescent or
steady-state tube
idle current flowing through
anode-to-cathode
resistance R1.

As
a positive-going
grid-to-cathode
RF voltage decreases
anode-to-cathode
resistance R1,
the magnetic flux
stored in
the inductance of RFC1 tries to hold
supply current
steady. RFC1 reacts
to the current
change by increasing
voltage across
its terminals.
Energy stored in the
electric field of C1
tries to hold the
voltage steady, and
C1 sources any
additional current
the tube (R1)
requires as it tries to force C2 and the tank input negative.

 

 

 

 

The
anode, in effect,
“tugs” or pulls
point A towards
ground. The initial
peak current can be
quite high, limited
only by
plate-to-cathode
resistance, because
C1 has a
low-reactance (at the operating frequency) path
to ground through
C2. The tank
inductor L1 also builds
up a magnetic field,
as plate tuning
capacitor C2 develops
a charge and
gradually increasing voltage.
This voltage
increase comes from the
current flowing
through C2 and C1
back to the tube. On
the initial RF
cycle, the voltages
hardly change before
the grid is moving
back negative.

At
a time interval
equal to 1/(4F)
(where F is the RF
frequency), the
positive grid
voltage has peaked.
The grid begins to
swing negative (or
less positive) with
respect to the
cathode.
Anode-cathode
resistance (R1)
decreases in step
with decreasing
grid-cathode
voltage.

There is no power-supply-forced
upward swing (the
tube cannot source
anything). The
collapsing field in
tank coil L1 (and to a much
lesser extent the collapsing field in plate choke RFC1)
tries to hold
changing anode current at the same
value. This is accomplished by the inductances of RFC1 and L1 increasing voltage as tube
anode-to-cathode resistance increases. L1
(and to a lesser
extent RFC1)
pull
anode voltage above B+ rail
by an amount virtually equal to the amount
anode voltage
was pulled downwards by the tube, with the anode even more than twice B+
rail voltage under some tank loading
conditions! 

The
actual amount the
tank pulls this
voltage higher than
+HV depends on the
amount of energy
transferred to the
load compared to
energy stored in the
tank system! This
is VERY important in
understanding where
arcs come from! Some
switching power
supplies, many
ignition coils used
in automobiles, and
the flyback systems
in television
receivers use this
type of “flyback
effect” voltage to
step up voltages to
very high levels
without use of
transformer action.

This
cycle repeats over
and over. Assuming the tank
system at C2, L1,
and C3 is resonant,
voltage at point
A increases in alternating swing
while the peak
current through R1
(the tube) is
gradually reduced.
Eventually, in
a fully loaded
amplifier,
equilibrium is
reached. In a properly
tuned amplifier
running at maximum
available power,
equilibrium occurs
when point “A”
swings up and down
an amount just under
twice the anode DC
voltage. 

Consider
a class AB 3-500Z
using a 3000-volt
supply. When the
amplifier is tuned
into the load
properly at full
rated power, and
driven to full
power, anode voltage
will swing between
5,500 volts maximum
and 500 volts
minimum at point A.
This would be a total
anode voltage swing
of 5,000 volts.
Peak instantaneous anode current
in continuous
carrier operation
would typically be
1.12 amperes, with a
minimum R1 value of
446 ohms. This is
typical of
continuous CW power
out of 750 watts
with a single 3-500Z
tube with a
190-degree
conduction angle
running at 400mA
average anode current from the HV supply.

Let’s
assume (we actually
CAN have this
condition, if the
amplifier and
exciter relays are
not sequenced
correctly) we have
an envelope that
rises instantly. At
the peak of first
positive
grid-cathode cycle,
the anode resistance
would drop to
someplace well under
400 ohms (anode
resistance is
non-linear with
anode voltage, and
is lower with higher
anode voltages). The
saturated anode
current could reach 7.5 amperes
in the 3-500Z,
if tube grid-cathode
bias
permits.

(Emission
in a directly heated
thoriated-tungsten
tube is typically in
the range of
50-100mA per watt of
heater power, large
transmitting tubes
being at the upper
end of that range. A
full-emission 3-500Z
has a saturated
emission current of
about 7.5 amperes.) 

If
we have infinitely
fast envelope rise
and fall times from
the exciter,
amplifier
RF-envelope rise and
fall times are
determined by the
operating Q of the
tank system.
C2/L1/C3 dominate
the high frequency
energy storage. RFC1
and C1, being larger
values, dominate
lower-frequency
energy storage,
while stored energy
in the power supply
dominates long-term
energy demands. The
voltage across C2,
upon initial
application of RF
drive, is a rapidly
expanding sine wave.
It reaches maximum
steady-state swing
many dozens or
hundreds of RF
cycles later than
the initial tube
excitation (and
decaying in a
similar fashion).

The
peak voltage across
C2 is equal to the
peak anode voltage
swing, and the
peak-to-peak voltage is
slightly less than
twice the HV supply
voltage in NORMAL
operation. The
voltage across C3 is
a function of the
load resistance, and
power delivered to
the load. 

 

SWR or Reflected Power Myth: We often hear people claim reflected power burns up as heat in the power amplifier stage. This is not true at all. The only effect of reflected power is it changes the loadline of the output device. This can either increase PA device RF voltage swing, or it can increase PA device current. If the voltage increases heat generally is reduced, but the PA can arc. If the load mismatch is of a phase angle that increases current, PA device heating increases because conduction angle and peak current increases. In one case heat increases, in the other heat decreases. An SWR mismatch only requires the matching network be readjusted to restore the proper loadline at the output device. In an adjustable pi-network or pi-L network system the only effect of SWR is in current in the inductor(s) and voltage across the loading capacitor, so long as the network can be adjusted to proper load at the output device. in other words if you can retune the network and don’t exceed voltage breakdown of the loading capacitor, your amplifier is very likely OK for any SWR.

Incorrect
Loading or Load

We
know the tank
circuit stores
energy. We now
understand the
conversion process
where DC is
converted to AC (or
RF) power. We also
must understand energy
must be transferred
out of the tank at a
rate equal to or
exceeding the rate
at which it is
supplied by the
downward “pull”
of the tube.
If we do not
remove energy at a
sufficient rate,
voltages and
currents increase
until a new point of
equilibrium is
reached. 
Voltage at
point “A” can
actually swing well
beyond twice +HV on
upward excursions,
and below zero volts
(becoming negative)
on downward
excursions.

The
maximum voltage with
a load or drive
fault can be
tremendously higher
under the fault
condition than typical
properly operating
tank working voltages
(when
energy is being
removed at the
proper rate). If we
do not remove energy
from the tank at the
same rate the power
supply is supplying
energy, the voltage
in the tank will
increase until
something absorbs
that energy!

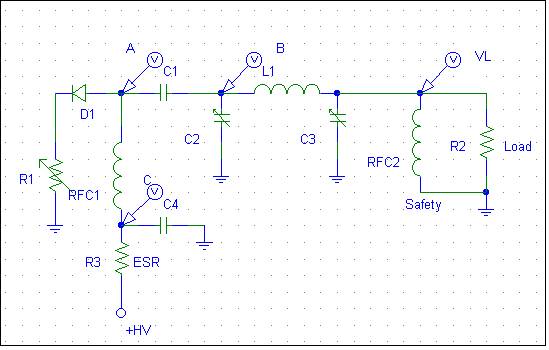
We
have the same basic
tank system as
discussed earlier,
but with light
loading compared to
drive level the
tank is pulled down
very hard by the
tube. Minimum Rp is
reached early in the
cycle, before the
tank voltage reaches
it’s minimum
swing. 
This is easy
to do, since the
tube only pulls the
system down and the
tank stores the
energy of that
downward tug.

As
the plate voltage
swings below zero
(negative) from the
tank energy, the
tube is already
cutting off. Nothing
clamps or prevents
point A from going
negative. D1
effectively takes
the tube out of the
circuit. By the time
the tank reaches it’s
minimum, the tube’s
grid-cathode voltage
is already on its
way positive. The
tank free wheels
positive, and can
overshoot the +HV
supply by several
times the supply
voltage. If loading
is light enough and
Q is high enough,
this continues until
the energy stored in
the tank reaches
equilibrium with
energy transferred
to the load, or a
component fails and
the arc dampens the
tanks gyrations.

See
the practical
demonstration
page for a real
working model with
waveforms!

 

 

 

 

 

Proper Plate Load
Impedance or
Operating Impedance
of an RF Amplifier

Since the
anode-to-cathode
resistance of the
tube varies over the
RF cycle, how do we
establish the plate
resistance of the
tube? It all goes
back to energy
transfer. We must
extract the same
energy available
from the power
supply power drawn
by the time-varying
tube resistance,
less any dissipation
in the tube or loss
in the tank
components.
Otherwise the anode
voltage swing will
not be in
equilibrium, voltage
swing will continue
to build until
something eventually
extracts the energy
at the same rate as
it is applied.

If
we try to extract
too much power to
the load compared to
the optimum value,
the output device
current will
increase. The tube
path looks like
this:

 

 

 

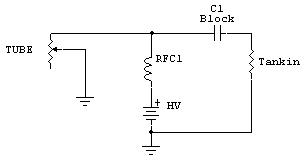
The
tank circuit
transforms the load
impedance of the
antenna system or
dummy load up to a
new value. This
resistance appears
at C1, and is
coupled through C1
to the tube and
power supply
junction. This is
the resistance value
we are actually
calculating when we
plan the plate
resistance, Rp.

 

 

 

This
resistance has to
match the optimum
E/I of the desired
RF frequency
appearing at the
anode of the tube.
Let’s consider the
fundamental
frequency only in a
typical class AB
amplifier operating
near the class B end
of the operating
point. Let’s assume
we have 3000 volts
of high voltage, and
the tube performs
best swinging down
from 3000 volts to
500 volts. This is
2500 volts of peak
anode voltage swing,
and the flyback
effect causes the
anode to reach 3,000
(B+ value) + 2,500
(downward swing) =
5,500 volts on peak.
Our vacuum tube has
a peak dc anode
voltage of 5,500
volts in
NORMAL
linear operation. If
you develop an
antenna system
problem or have a
bad lightning
arrestor or relay,
the peak voltage
could be several
times that amount.

I’ve seen test data from Chinese 572B’s where the tubes were tested for arcing and failure at 1,500 volts dc anode voltage. If we think about this, all tubes should be tested to withstand some significant amount more than twice the maximum dc anode voltage. This is a noteworthy point because test data from various Chinese manufacturers has indicated they test tubes at less than the rated dc supply voltage. Manufacturers should actually be testing and gettering tubes to withstand significantly more than twice the highest expected dc supply voltage. Even an 811A should not be tested that low. The old Eimac 3-500Z’s, rated at 4,000 volts supply voltage, used to test to over 12,000 volts of anode-to-grid breakdown voltage. They virtually never arced when new. To be reliable an 811A tube should hold off nearly 5 kV with minimal leakage and no sign of arcing. A 572B should hold off over 8,000 volts.

With
the 3-500Z example,
we might have a
useful RF output
power of 800 watts
with the anode
swinging 2500 volts
peak (5000 volts
p-p), or about 1700
volts RMS at the
fundamental. There
are harmonics
involved, so to do
this right we would
have to use a
Fourier (harmonic
waveform) analysis
of the waveform, and
there is just such
an analysis that was
developed for vacuum
tubes called a
Chaffee analysis,
but for casual use
we can use
approximations. The
typical rule of
thumb for tubes with
a 15% minimum plate
voltage is we
multiply indicated
anode current 
by 1.6, and use the
supply voltage.
Ep/(Ip*1.6) = Rp.
Using this example
we have
3,000/(.4*1.6) =
4,688 ohms.

Now
let’s look at
another rough
method. We know the
swing is about 2500
volts, so RMS is
about .7 times that.
1750^2 / 750 = 4,083
ohms.

Using a Chaffee
analysis the optimum
load resistance
comes out to 4500
ohms. The error in
approximations is in
not allowing for
harmonic content.

Tank Q

We
often get far too
worried about tank
circuit Q. There
really is very
little change in
efficiency as Q
moves from a minimum
of (SQRT Rp/Rl)+1.
If we had a 4500 ohm
optimum anode load
resistance (Rp) and
a minimum load
resistance of 25
ohms, we would want
a tank Q of at least
SQRT 4500/25= 13.4 +
1 = 14.4. A 
typical HF tank
circuit, even with
modest sized
components and such
a large impedance
ratio, only has
approximately 4 %
power loss. If we
doubled the Q, tank
loss would only be 8
%. Lower impedance
ratio tanks have
even less loss and
are less worrisome.

Most
of the power loss is
in the conduction
angle and waveform shape of the tube,
not tank Q. It is
certainly not in a
blocking capacitor,
would would overheat
and disintegrate if
it had more than a
tiny fraction of
just one percent
loss.

Don’t get overly
concerned about Q.
Most of the time you
will be off 20-30%
anyway. Handbook formulas
for Q and Rp are
just rough
approximations, and loaded-Q generally has a small effect on overall efficiency
(unless the tank components have a great deal of loss).

Efficiency

The efficiency of a power amplifier can be well over 50% even when the
amplifier’s output port is conjugate matched to the load. This is because the
output device can switch on and off hard, and not be in a state where it looks
lie a dissipative resistance very long. The tank circuit filters the sharp
transitions out, and rounds the waveform into a sine wave. At this point we have
an optimum across and through vector, voltage across the tank and current
through the tank, and that is the “impedance” conjugate matched to the load.
The only dissipative part of the system, other than small tank and circuit
losses, is the tube or output device. Since that area is non-linear (not in
transfer function, but in fractional cycle linearity) power conversion
efficiency can be quite high.

As an example of this I measured the output impedance of a pair of class-C
6146’s two ways, by using a traditional load pull and by using a reverse power
generator and a tapped line. When tuned for maximum efficiency at full power,
the output port looked very close to being a 50-ohm source. Despite being a
50-ohm source, efficiency was around 80%! As a matter of fact I measured over a
dozen PA systems and all of them produced near-maximum efficiency and an
efficiency of over 50% while they behaved like a true 50-ohm source.

An amplifier does not need to be conjugate matched to work, and indeed many or
most are not conjugate matched, but they are when tuned for maximum
efficiency!

To have high efficiency conduction angle must be as short as possible, and when
the output device turns off (goes open circuit) the output device must
transition into open circuit as rapidly as possible. This is why a
low-pass tuned input is so
necessary for maximum efficiency in a grounded grid amplifier.

Reflected Power

Contrary to somewhat popular myth, reflected power does not heat the power amplifier. As
a matter of fact reflected power can actually make the PA stage run cooler! The
only effect of load mismatch is the operating load line presented to the output
device by the tank circuit shifts to a different value. Normally, an adjustable
tank has enough range to correct the load line change. Even if the SWR is 10:1,
if the tank adjustment range allows adjustment to normal grid and anode currents
and proper RF power levels, efficiency and heating will not change.

If tank range is insufficient for the impedance presented to the PA by the
feed line, or if the PA stage is “fix tuned” and lacks any ability to readjust to
a new load impedance value, the load line will shift. To the tube or output
device, this is not any different than mistuning the tank. This is why
non-adjustable systems, like typical solid state PA’s, require a low “load SWR”.
Because the tank cannot readjust, they must see the design impedance. This is
typically 50 j0 ohms.

If  loadline impedance decreases, the output device’s current
will increase. The current increases while peak output device voltage is reduced,
and the anode current conduction angle increases. The longer time period of
increased current result is more anode heat. This can result in an anode
thermal failure, if the time and dissipation product exceeds safe
limits.

If the loadline changes in a way that reduces anode current, less
anode heating occurs. The output device runs cooler,
but peak voltage increases. If
peak voltage exceeds safe limits, an instantaneous failure will occur.

Tube-type amateur transmitters were often rated for a very wide
load impedance range. This shows the fallacy of thinking feed line reflected
power causes a PA to overheat.