|
An
Intuitive
Explanation of CW
Bandwidth
by Mark Amos,
W8XR
How much bandwidth
does it take to send
Morse code?
When the question of
CW* bandwidth is
discussed there are
often
inconsistencies and
inaccuracies
sprinkled in among
the facts. And,
while technical
explanations can be
found, they are
typically laced with
difficult
mathematics. In
researching the
topic, I found that
there was a lack of
simple, intuitive
explanations. I
hope this article
serves that need.
Topics that well
cover:
–
Production of
radio frequency CW
–
Morse Code
keying
–
The keying
envelope
–
Rise and fall
times
–
Keying speed,
baud rates
–
Carrier
bandwidth
–
CW bandwidth
First, some basic
foundation material
about radio, Morse
code speed, baud
rates and keying for
those of you who
havent spent much
time in this arena.
What does it take to
send Morse code via
radio waves?
–
some kind of
a radio frequency
oscillator to create
a carrier frequency
–
an amplifier
to buffer and
amplify the
oscillator output
–
a feed line
and antenna to
couple the signal
from the amplifier
to the void
–
a way to turn
that carrier (CW*)
on and off to
transmit Morse code.
We wont talk about
the first three
here. There are
plenty of good books
and websites that
explain them well
the ARRL Handbook is
a great place to
start.
One obvious way to
turn the carrier on
and off is to use a
key between an
oscillator and an
antenna.
Alternatively, as in
some early radios,
the key might turn
an oscillator on and
off as we tap out
our message. Or, it
might interrupt the
signal from the
oscillator to the
amplifier. It could
also turn the
amplifier on and
off. It could use a
combination of
these. Regardless
of how its done,
this keying is what
imparts information
onto an otherwise
steady (and
information free)
carrier.
A key is a switch
its either on or
off. If you were to
tap out a series of
dits on a key hooked
up to your
transmitter and look
at the keys
terminals with an
oscilloscope youd
see something that
looks like a square
or rectangular
wave. If youve
been around long
enough, you might
even have heard one
or two radios that
had oscillators or
amplifiers that were
directly keyed.
Modern radios
modify the shape of
this keying waveform
so that it doesnt
turn on and off
instantaneously.
Its transitions are
rounded off so that
they are less
abrupt. Well be
talking a lot about
this shape. Its
often referred to as
the keying
envelope.
In Morse code there
is a standard word
used in speed
measurement. Its
made of the letters,
PARIS. If it
takes you one minute
to send PARIS, then
youre sending at
one word per
minute. The dits,
dahs and spaces of
PARIS add up to
exactly 50 element
lengths long (Figure
1.) (The last seven
empty elements are
an inter-word
space.)
°”/>
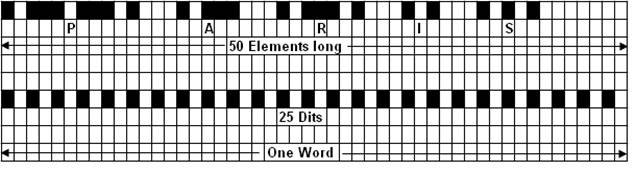
Fig. 1. Standard
word PARIS and a
simpler test word
Of course there are
many possible
combinations that
would result in a 50
element length word
PARIS is just one
that is used as a
standard.
For the analysis
below we will use an
alternative and very
simple 50 element
length word: a
string of 25 dits.
Add up all the dits
and the separating
spaces and you get a
50 element length
word. You could use
any test word
ultimately the
results would be
similar but this
simple 25 dit string
might make the
following discussion
a little easier to
understand.
If we send our test
word at the
ridiculously high
speed of 60 WPM
(Words Per Minute)
we get one word per
second.
If you had a
computer before high
speed internet
access was the norm,
you used a modem.
Modem speed is
measured in terms of
baud rate.
Typical baud rates
for modems started
out at 110 baud in
the 1970s and
increased quickly
through 300, 1200,
9600, 192000 and
56000 baud in the
90s. How fast is
60 WPM in terms of
baud? This requires
a look at the
technical definition
of baud. Its
not critical that
you understand baud
rate Im just
providing this
information for
comparison purposes.
One baud is equal to
one bit of
information (or one
state change) per
second. There are
two state changes
per dit in our test
word one where the
carrier turns on,
the other where it
turns off.
While there are
people that can copy
code faster than
this, there arent
many. The record is
just over 75 WPM.
Our test word at 60
WPM is about the
cross-over point
where other digital
modes start making
more sense than the
on/off keying (OOK)
of Morse code.
A common conversion
factor for WPM to
baud is .83. So, 60
WPM * .83 is about
50 baud. 12 WPM is
about 10 baud. One
of the slowest RTTY
baud rates (45.45
bauds) is close to
our 60 WPM test
keying rate. (In
computer signaling,
the term bps has
replaced baud as a
transmission speed
measurement. This
can get confusing
because it is
possible to encode
more than one bit
into a state
change. Well
ignore that
complication for
this discussion.)
You might be
thinking, Well, if
baud is state
changes per second,
then wouldnt real
Morse code words
have different baud
rates than this test
word at 60 WPM?
Yes, in fact there
could be many 50
element length words
each with different
baud rates because
of the different
number of
transitions. Morse
code has variable
length letters so
the conversion to
baud and bits per
second is a bit
odd. But it doesnt
really matter to
this discussion, so
well ignore this
complication too
Ive only mentioned
it here to give you
a frame of
reference. If you
need to do a WPM to
BAUD conversion,
just use .83 bauds /
WPM and youll be
close.
When we send our 25
dit test word at
60 WPM, we will key
and un-key the
carrier 25 times per
second (25 Hz, or
25 cycles per
second .)
One way to think of
this is that were
amplitude
modulating our
carrier with a 25 Hz
keying envelope.
Just turning the
carrier off and on
is a very simple
type of modulation.
Its also very noisy
and inefficient it
requires a lot of
bandwidth. Well
talk about how much
bandwidth a little
later.
However, as we know,
Morse code can
be a very bandwidth
efficient medium if
were careful.
Being conscientious
amateurs, we would
never key our
transmitter with a
square (on/off)
keying envelope.
That would be
seriously hard
keying the kind
that causes annoying
key clicks.
Instead lets try a
softer kind of
keying, rounding off
the sharp corners of
this square, on/off
keying envelope.
In fact, lets start
with the softest
possible keying.
Well use a raised
cosine shaped wave
for our keying
envelope. It will
gently increase our
carrier from 0 to
100% and then back
down again.
Technically, the
softest possible
shape is actually a
Gaussian noise
curve. As shown in
Figure 2., they are
really the same
shape with different
names.
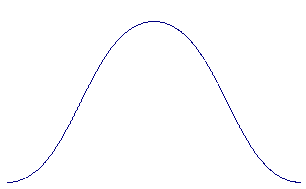 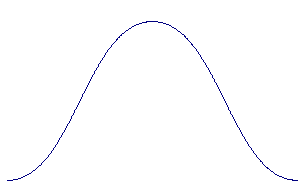
Fig. 2 Raised Cosine
Waveform
Fig. 3 Gaussian
Waveform
So, using the very
soft keying envelope
from Figure 2 (or
Figure 3
), the
carrier starts out
with zero amplitude,
slowly rises, and
accelerates as it
climbs through 50%.
Then its rate of
climb decelerates
until it gets to
100% carrier
amplitude. This
rise from 0 to 100%
forms a kind of
S-shaped curve (a
sinusoidal curve.)
After reaching
100%, it begins to
drop off. This
drop-off accelerates
down through 50% and
finally the rate of
change slows down as
the end of the
keying envelope is
approached. The
changes to the
amplitude of the
carrier are smoothly
changing throughout.
If we do this in 40
milliseconds, we
will have sent one
dit at 60 WPM
(well do the
calculation for this
a little later.)
This would be
impossible for a
human to copy. If
we sent 25 of these
(our test word), at
60 WPM the sound
would run together
and the result would
be an unintelligible
25 Hz hum. (Under
laboratory
conditions, using a
computer with
digital signal
processing software,
the computer might
be able to read
these 25 dits, but
not you or I.)
In any case,
copy-able or not,
this keying envelope
results in the
minimum possible
bandwidth necessary
to key a carrier at
60WPM.
Lets not confuse
this minimum
possible bandwidth
with bandwidth
required for
readability. What
were talking about
here is the minimum
possible bandwidth
that occurs when you
key a carrier at 60
WPM with a raised
cosine keying
envelope. (Well
talk about bandwidth
required for
effective receiving
some other time.)
So, how much
bandwidth does
it take? We need
some simple mixer
theory to talk about
this.
As you should
remember from
studying for your
amateur license,
when you modulate
(or mix) one signal
with another, you
get the sum and
difference of the
two signals. Often
the two original
frequencies tag
along and the
modulating signal is
typically removed by
filtering.
So, a 1 MHz carrier
modulated by this
soft 25 Hz keying
waveform, results in
4 resulting
frequencies:
1.) 999,975 Hz (the
difference: 1 MHz –
25 Hz)
2.) 1,000,025 Hz
(the sum: 1 MHz + 25
Hz)
3.) 1,000,000 Hz
(the carrier)
4.) 25 Hz (the
modulation
frequency) this
signal wont make it
out of your
amplifier, much less
your antenna
So, the bandwidth
this mixed signal
uses is: 1,000,025 –
9,999,975 = 50 Hz.
The sum and
difference signals
are what create the
sidebands of the
signal. The sum
results in the upper
sideband and the
difference makes up
the lower sideband.
The carrier in the
middle doesnt take
up any bandwidth
(and doesnt contain
any information.)
As I said, using
this soft keying
envelope, Morse code
would be extremely
difficult for other
people to copy. In
order to make it
more readable, we
need to harden the
keying.
For now, lets use
rise time and fall
time to describe the
keying hardness.
(The shape of the
rise and fall is
important too but
well keep the shape
constant for now and
continue to use
parts of a raised
cosine shaped
envelope.)
Using the softest of
all possible keying
envelopes, the
Gausian envelope,
the rise time for a
dit is 20 mS and the
fall time is 20 mS.
When we send a
string of 25 of
these dits, this
makes up what
amounts to a 40 mS
wavelength. (We can
check our work by
taking the
reciprocal of the
frequency to get the
wavelength that is
we divide 1 by 25.
This comes out to
.040 seconds or 40
mS; half of it is
rise time and half
of it is fall time
(Fig. 4.)
For this kind of
soft keying, well
call anything above
50% on and
anything below 50%
off.
°”/>
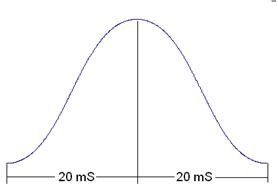
Fig. 4 One Dit at
60 WPM (25 Hz keying
envelope.)
What if we halve the
rise time and fall
time to 10 mS but
leave the frequency
the same?
Well get (Figure
5.):
10 mS rise time
10 mS where the
signal is at 100%
10 mS fall time
10 mS with the
signal at 0.
Since the frequency
is the same, 25 Hz,
this whole envelope
has to add up to 40
mS. Weve just sort
of stretched out
the parts of the
envelope where the
carrier is 100% and
where its 0%. But
weve also narrowed
the raised cosine
parts for a sharper
rise and fall. See
figure 5.
ì”/>
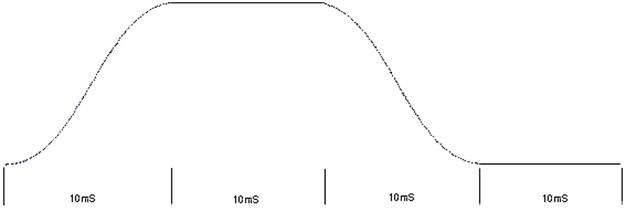
Figure 5. 10 mS
rise, 10 mS at 100%,
10 mS fall and 10 mS
at 0
(Still 25 Hz 60
WPM)
During the times
when the envelope is
steady (at 100% and
0) the carrier is
not taking up any
bandwidth: if
we transmit an
unchanging 1MHz
carrier it wont
take up any
bandwidth. This is
difficult for a lot
of people to
accept. It seems
counterintuitive
(There must be
SOMETHING there
taking up
bandwidth), but
its true.
Put another way: the
only time that the
sidebands push out
and take up
bandwidth is during
a change in
the amplitude of the
carrier. That is,
during the time that
the envelope is
going up or down
(where the amplitude
of the carrier is
increasing or
decreasing.)
Ideally, when
transmitting CW,
this only happens
during the rise time
and fall time of the
keying envelope**.
Even this smooth
raised cosine
envelope changes the
amplitude of the
carrier, albeit
slowly and
gracefully no
jagged edges here.
This changing
envelope causes
the sidebands to
push out either side
of the carrier.
OK, now lets dig
just a little
deeper.
The width of the
sidebands (the
bandwidth) has to do
with the steepness
of the keying
envelope; how fast
it is changing the
carriers
amplitude. By
increasing the
slop of
our keying waveform,
were increasing the
required bandwidth.
Signaling theory
folks would argue
that its the rate
of modulation the
25 Hz modulating
signal in our
example that
causes the
sidebands. Ive
heard a number of
arguments about this
assertion.
Youre welcome to
look at it this way,
but consider this:
what is really
changing when the
modulation rate
changes? Its the
steepness of the
rise time and fall
time of the keying
envelope. Heres an
example.
What if we double
our initial keying
rate from 60 WPM
to120 WPM (that is,
increase our
modulating frequency
from 25 Hz to 50
Hz)? What would the
leading and trailing
edges look like?
This is easier to
see than it is to
talk about. Take a
look at a 25 Hz
cosine shaped wave
overlaying a 50 Hz
cosine shaped wave
in Figure 6.
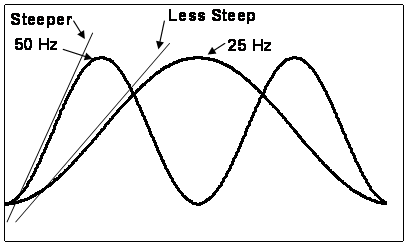
Fig. 6 Its the
Steepness that
counts.
Notice anything
interesting about
how steep the 50 Hz
wave is as it goes
from 0 to peak?
You might say the
rate of change is
twice as steep as
in the 25 Hz wave
and youd be right.
In order to fit 50
cycles into the same
second that our 25
Hz signal fits in,
each 50 Hz wave has
to have steeper
sides than the 25 Hz
waves in fact,
twice as steep.
Again, its the
rate of change of
the carrier due to
the keying envelope
that counts. The
slope, or the rate
of change, is a
measure of the
steepness of the
rise or fall time.
For a modulating (or
keying) waveform,
twice as steep means
twice the bandwidth.
Some might still
argue that the
increase in the
modulation rate is
causing this.
Of course theres a
kernel of truth
there. If you
increase the rate of
modulation, you
increase the
steepness of the
modulating wave form
(as is evident in
Figure 6.) But,
its actually the
steepness of the
rising and falling
envelope that causes
the sidebands (and
consequent
bandwidth) not the
signaling rate. If
you had only one
wave at this
frequency, the
bandwidth required
would be exactly the
same as the
continuous train of
waves in our
example.
Technically, its
not just the
steepness of the
rise time and fall
time. More
precisely, its the
rate of change of
any part
of the envelope.
For instance, if
instead of a nice
smooth rise from 0
theres an abrupt
change, this abrupt
change will increase
the bandwidth. A
saw-tooth,
triangular or
stepwise envelope
would cause a much
higher bandwidth
signal than our
raised cosine
envelope. If the
carrier is modulated
in some other way
the bandwidth could
also increase (for
instance if the
signal has some
chirp) but in this
analysis were only
considering
bandwidth due to the
keying envelope.
You need to get to
the point where you
can say, with
conviction: Its
the shape of the
keying envelope that
causes a keyed CW
signal to take up
bandwidth. An
un-keyed/un-modulated
CW signal takes up
no bandwidth.
How can we determine
how wide our signal
will be based on the
rise and fall times
of the keying
envelope? This
section talks about
a way to estimate
this.
When we harden the
keying by increasing
the slope of the
rising or falling
part of the keying
envelope, were
pushing out the
sidebands as if
we were modulating
our carrier with a
wave that has the
same slope and shape
as the rising and
falling parts of the
modulation
envelope. This is a
little tricky, but
an example should
help.
In the first
scenario above, we
halved the rise and
fall time to 10 mS
apiece but kept the
keying rate the
same. By cutting
the rise and fall
time in half, its
as if were
now modulating our
carrier with a 50 Hz
sine wave (even
though the rise time
and fall time are
separated by periods
of no change.) The
sidebands push out
to +- 50 Hz,
requiring 100 Hz of
total bandwidth to
send this same 60
WPM word.
Another way to say
this: if we keep the
rise time and fall
time of our envelope
and take out any
parts where the
envelope is not
changing (when its
at 100% and 0% for
instance), we can
figure out this
waveforms frequency
(based on its
wavelength) and use
that to estimate
required bandwidth.
So, for instance, a
50 Hz sine wave has
a rise time and fall
time of 10 mS each
(1 / 50 is
20 mS.)
If our
envelope has the
same rise time and
fall time as a 50 Hz
sine wave, and its
rise and fall have
the same shape as
the rise and fall of
a 50 Hz sine wave,
then we can treat it
like a 50 Hz signal
to compute
bandwidth.
Remember: when
the keying envelope
isnt changing,
there are no
sidebands and no
bandwidth
sidebands and
bandwidth only
occur during the
times when the
keying envelope is
changing.
If we halve the rise
and fall times again
(to 5 mS), its as
if were modulating
our carrier with a
100 Hz waveform (5
mS rise time + 5 mS
fall time = 10 mS;
1/10 mS = 100 Hz).
The sidebands go out
to +- 100 Hz for a
total of 200 Hz
bandwidth.
Of course in the
real world, not many
radios use smooth
Gaussian keying, as
we do here.
Typically they use a
resistor-capacitor
filter used to
soften up the rise
and fall. Why is
this still done?
The engineering
isnt that hard
anymore – its a
matter of economics:
it would cost more
per radio for
manufacturers to add
a Gaussian keying
envelope.
An RC filter has
sharper edges and
consequently causes
more bandwidth to be
used. Its
obviously better
than just using a
square keying
envelope. However
its still pretty
wide and if the rise
time and fall
times are less than
5mS or so, it will
be pretty clicky
even on some
high-end radios.
Ok, so how much
bandwidth would a
square keying wave
take?
Way too
much. The rise and
fall times of a
square wave are
infinitely steep.
This kind of keying
results in a very
wide signal with
lots of noise with
every key down and
key up.
Its as if youre
modulating your
carrier with a very
high frequency
signal sidebands
are pushed out to
infinite bandwidth.
Well, maybe not
infinite, but a lot
more than the other
amateurs up and down
the band deserve. If
youre doing this on
40 meters, some of
your key clicks
could be making it
up to the 20 meter
band — or maybe
even your phone or
your neighbors TV,
depending on how
much power youre
trying to pump out.
Not only is this
inefficient there
is wasted power in
those infinite
sidebands in most
parts of the
civilized world its
illegal. The exact
bandwidth is tricky
to calculate,
because of things
like the bandwidth
of your transmitter,
filters that might
be in the signal
path, your amplifier
linearity, the width
of the pass-band of
your tuner, the
bandwidth of your
antenna, etc.
Regardless, its
wide enough to get
you in trouble. So
pay attention to
your keying
envelope. Dont key
that homebrew rig
with a square
envelope or any
envelope that has a
rise
time or
fall time less than
5 mS or so. Also,
if possible the rise
and fall should be
shaped like our
raised cosine curve.
If theyre
exponential curves
(like you get with
an RC filter) you
will be taking up
more bandwidth than
is absolutely
necessary.
Here are a couple of
key takeaways:
–
If you take
nothing else from
this article, you
should be able to
say with confidence
The bandwidth of a
typical CW signal
depends on the shape
of the keying
envelope.
–
The hardness
of the keying is
greatly influenced
by the rise and fall
time of the keying
envelope. A rise and
fall time of 5mS or
more will result in
a readable signal at
reasonable
bandwidth.
–
Sidebands of
a CW signal are
caused by keying (an
unmodulated carrier
requires no
bandwidth.)
–
You can
estimate the
bandwidth required
by analyzing the
shape of the keying
envelope (removing
the parts that are
unchanging and
calculating the
frequency of the
remaining portions.)
This applies with
soft keying.
Using harder
keying increases the
required bandwidth
dramatically.
–
Lots of
people like to argue
about these points
even if they dont
really understand
them. Its best to
just walk away
from these
arguments, unless
you just like to
argue. Little
exchange of
knowledge is likely
to occur, even if it
is somewhat
entertaining
*Technically, CW
means Continuous
Wave. When radio
amateurs talk about
CW theyre really
talking about
on/off keying (OOK)
of a continuous
wave. Certainly
theres nothing
continuous about a
keyed carrier; it
stops and starts all
the time. As
mentioned above
technically, CW
doesnt take ANY
bandwidth at all if
its not being
modulated. In this
article, we use the
term CW in the
amateur sense.
**Of course in the
real world there are
complications, like
phase noise, jitter,
FM, etc. but thats
another story and
doesnt really add
to this discussion
in any meaningful
way.
|





